Trọng tâm là gì? Công thức tính trọng tâm của tam giác

trọng điểm là gì, công thức tính trung tâm của tam giác như thế nào? Mời các bạn đọc bài viết dưới đây để hiểu thêm về trọng tâm tam giác, tri thức rất quan yếu và phổ biến trong những niên học phổ biến nhé.

trọng tâm là gì?

Một tam giác có 3 đường trung tuyến, đoạn thẳng nối từ đỉnh của tam giác đến trung điểm của cạnh Trong cuộc sống, giai đoạn khó khăn nhất không phải là không ai hiểu bạn, mà là… bạn không hiểu chính mình. đối diện.

trung tâm của tam giác là giao điểm của ba đường trung tuyến.

G là trung tâm của tam giác ABC.

thuộc tính của trọng điểm trong tam giác

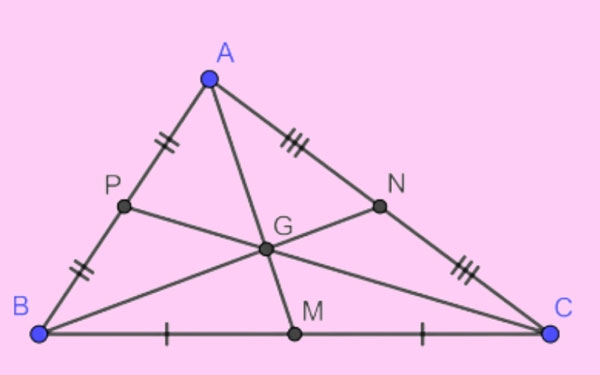
Khoảng cách từ trung tâm của tam giác đến đỉnh bằng 2/3 độ dài đường trung tuyến ứng với đỉnh đó.

Tam giác ABC, với các đường trung tuyến AM, BN, CP và trung tâm G, ta có: GA = 2 AM GC = 2 GP BG = 2 GN

trung tâm tam giác vuông

trung tâm của tam giác vuông cũng được xác định giống như trung tâm của tam giác thường.

Tam giác MNP vuông tại M. 3 đường trung tuyến MD, NE, PF giao nhau tại trọng tâm O. Ta có MD là trung tuyến của góc vuông PMN nên MD = 1/2 PN = DP = DN.

trung tâm tam giác cân

Tam giác ABC cân tại A, có G là trọng điểm. Vì tam giác ABC cân tại A nên AG vừa là đường trung tuyến, đường cao và là đường phân giác, từ đó ta suy ra được hệ quả của trọng điểm tam giác cân ABC như sau: Góc BAD bằng góc CAD. Trung tuyến AD vuông góc với cạnh đáy BC.

trọng điểm của tam giác vuông cân

Có tam giác ABC vuông cân tại A và I là trọng điểm. AM là đường trung trực, đường trung tuyến và đường cao của tam giác này nên AM vuông góc với BC. Mặt khác, vì tam giác ABC vuông cân tại A nên: AB = AC. => BP = CN và BN = AN = CP = AP.

trọng tâm tam giác đều

Tam giác ABC đều, G là giao điểm ba đường trung tuyến, đường cao, đường phân giác. nên theo thuộc tính của tam giác đều ta có G vừa là trọng tâm, trực tâm, tâm đường tròn ngoại tiếp và nội tiếp của tam giác ABC.

Cách tìm trọng tâm tam giác

Cách 1: Giao điểm 3 đường trung tuyến

Xác định trọng tâm tam giác bằng cách lấy giao điểm của ba đường trung tuyến.

Bước 1: Vẽ tam giác ABC, tuần tự xác định trung điểm của các cạnh AB, BC, CA. Bước 2: Nối tuần tự các đỉnh đến trung điểm của cạnh đối diện. Nối A với G, B với F, C với E. Bước 3: Giao điểm I của ba đường trung tuyến là AG, BF, CE là trọng tâm của tam giác ABC.

Cách 2: Tỉ lệ trên đường trung tuyến

Xác định trung tâm tam giác dựa trên tỉ lệ đường trung tuyến.

Bước 1: Vẽ tam giác ABC, xác định trung điểm M của cạnh BC. Bước 2: Nối đỉnh A với trung điểm M, sau đó lấy điểm S sao cho AS = 2/3 AM. Theo thuộc tính trọng điểm tam giác thì điểm S chính là trọng tâm tam giác ABC.

Bài tập về trung tâm tam giác

Bài 1 : Tam giác ABC có trung tuyến AD = 9cm và trọng điểm I. Tính độ dài đoạn AI?

Giải:

Ta có I là trung tâm của tam giác ABC và AD là đường trung tuyến nên AI = (2/3) AD (theo tính chất ba đường trung tuyến của tam giác). Do đó: AG = (2/3).9 = 6 (cm). Vậy đọan AI có độ dài 6 cm.

Bài 2:

Cho I là trọng tâm của tam giác đều MNP. Chứng minh rằng: IM = IN = IP.

Giải:

Gọi trung điểm MN, MP, PN tuần tự là R, O, S. Khi đó MS, PR, NO đồng quy tại trọng điểm I. Ta có ∆MNP đều, suy ra: MS = PR = NO (1). Vì I là trung tâm của ∆ABC nên theo tính chất đường trung tuyến: MI = 2/3 MS, PI = 2/3 PR, NI = 2/3 NO (2). Từ (1) , (2) ⇒ GA = GB = GC.

Ngoài trung tâm, tam giác còn có các kiến thức khác như diện tích tam giác , chu vi tam giác , đường cao tam giác , mời các bạn tham khảo.